مخروط یک شکل هندسی سه بعدی است که شبیه یک هرم است و یک پایه دایره ای دارد و به نوک تیز به نام راس ختم می شود.
اندازه مخروط چقدر است؟
حجم مخروط به عنوان مقدار یا حجم فضایی که شکل اشغال می کند تعریف می شود . حجم مخروط بر حسب واحدهای مکعبی مانند سانتی متر مکعب، متر مکعب، اینچ مکعب و غیره اندازه گیری می شود. یک مخروط را می توان با چرخاندن یک مثلث به دور هر یک از رئوس آن تشکیل داد. مخروط یک جامد سه بعدی با پایه دایره ای است.
مخروط ها را می توان به دو نوع مخروط دایره ای راست یا مخروط مایل طبقه بندی کرد. در مخروط دایره ای راست، راس عمودی بر روی قاعده قرار دارد، در حالی که در مخروط مایل، راس عمود بر مرکز پایه نیست.
فرمول محاسبه حجم مخروط
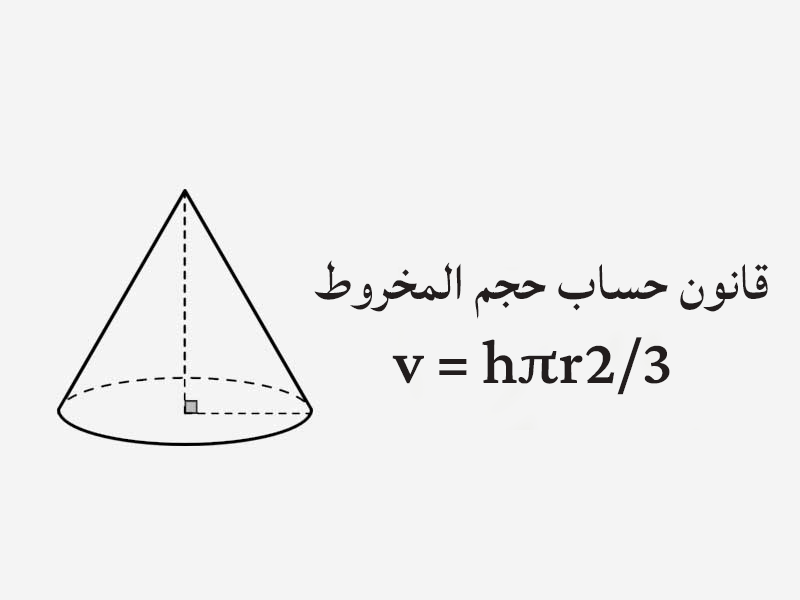
با یافتن ارتفاع و شعاع مخروط، می توانید به راحتی حجم مخروط را با اتصال این اندازه ها به فرمول محاسبه حجم مخروط محاسبه کنید. فرمول محاسبه حجم مخروط به صورت زیر است:
v = hπr 2/3
فرمول دقیق حجم مخروط به صورت زیر است:
V = (1/3) × π × r 2 × ساعت
- V: حجم مخروط را نشان می دهد،
- π : یک مقدار ثابت تقریبا برابر با 3.14159 است،
- r: شعاع قاعده مخروط است
- h: نشان دهنده ارتفاع مخروط است.
نمونه هایی از محاسبه حجم مخروط
فرض کنید مخروط دارای شعاع r = 3 سانتی متر و ارتفاع h = 8 سانتی متر است.
برای محاسبه حجم مخروط با این مقادیر باید از فرمول زیر استفاده کنیم V = (1/3) x π x r2 x h.
V = (1/3) × π × (3)^2 × 8
v = (1/3) × π × 9 × 8
V = (1/3) × π × 72
v = 72/3 × π
V ≈ 24 × 3.14159
v ≈ 75.398 سانتی متر مکعب
بنابراین حجم یک مخروط با شعاع 3 سانتی متر و ارتفاع 8 سانتی متر تقریباً 75.398 سانتی متر مکعب است.
قانون حجم مخروط شکسته
همانطور که در ابتدای مقاله اشاره کردیم مخروط ها انواع مختلفی دارند و یکی از آنها مخروط ناقص است اما برای محاسبه این نوع چه باید کرد؟ پاسخ اینجاست، ما باید از قانون زیر استفاده کنیم:
V = (1/3) × (A1 + A2 + √(A1 × A2)) × h
اینجا :
- A1 = مساحت اولین پایه مخروط.
- A2 = مساحت پایه دوم مخروط.
- h = ارتفاع مخروط.
حجم مخروط سرخورده را پیدا کنید
پایه های مخروط فروستوم دو مربع به طول 13 سانتی متر و 10 سانتی متر است. در حالی که ارتفاع مخروط گم شده 16 سانتی متر است. حجم مخروط ناامید کننده را محاسبه کنید.
پاسخ:
با توجه به اطلاعات ارائه شده:
- پایه اول مخروط: 13 سانتی متر
- پایه دوم مخروط: 10 سانتی متر
- ارتفاع فروستوم: 16 سانتی متر
با استفاده از فرمول زیر می توانیم حجم فروستوم را محاسبه کنیم:
حجم فروستوم = 1/3 x (مساحت پایه اول + مساحت پایه دوم + ریشه دوم حاصلضرب (مساحت پایه اول x مساحت پایه دوم) x ارتفاع
حجم مخروط فروستوم = (1/3) x (169 سانتی متر مربع + 100 سانتی متر مربع + ریشه مربع 169 سانتی متر مربع و 100 سانتی متر مربع) × 16 سانتی متر
اکنون می توانیم جذر حاصلضرب 169 و 100 را محاسبه کنیم:
محاسبه ریشه مربع:
√(169 سانتی متر مربع x 100 سانتی متر مربع) = √16900 سانتی متر مربع = 130 سانتی متر مربع
حجم مخروط شکسته = (1/3) x (169 سانتی متر مربع + 100 سانتی متر مربع + 130 سانتی متر مربع) × 16 سانتی متر
= (1/3) x 399 سانتیمتر مربع x 16 سانتیمتر
= 21312 سانتی متر مربع
بنابراین حجم مخروط فروستوم با داده های ذکر شده تقریباً برابر با 21312 سانتی متر مربع است.
نتیجه
توصیه می کنیم علاوه بر حل مثال های مختلف، اطلاعات کافی در مورد مساحت مخروط و همچنین موضوع روز یعنی حجم مخروط به دست آورید، زیرا مباحث مهندسی به دلیل قوانینی که نیاز دارند تا حدودی دشوار است. تمرین.